Молекулярная динамика белков и пептидов
Методическое пособие
1. Введение в метод молекулярной динамики.
1.1. Физические основы метода молекулярной динамики.
В основе методов молекулярной динамики лежит модельное представление о многоатомной молекулярной системе, в которой все атомы представляют собой материальные точки [1,2]. Причём, поведение отдельного атома описывается классическими уравнениями движения и имеет вид:
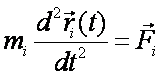(1)i – номер атома (1 ≤ i ≤ n), n – полное число атомов в системе, mi - масса атома,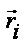 
– радиус-вектор атома, 
– равнодействующая сил, действующих на атом.
– радиус-вектор атома, 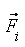– равнодействующая сил, действующих на атом.Равнодействующая сила складывается из двух составляющих:
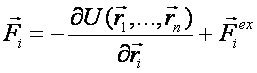(2)U – потенциальная энергия системы,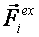 
– сила, определяемая взаимодействиями с молекулами среды.
– сила, определяемая взаимодействиями с молекулами среды.Первая составляющая – сила, действующая на данный атом со стороны всех остальных атомов. Взаимодействие между атомами является потенциальным, и поэтому первая сила записана как градиент потенциальной энергии системы. Некоторые способы введения дополнительных сил рассматриваются в следующем разделе.
Потенциальную энергию системы можно представить в виде суммы вкладов от различных типов взаимодействий между атомами [3]:
(3)Ub – потенциальная энергия валентных связей (4), Uv – валентных углов (5), Uφ – торсионных углов, Uf – плоских групп и псевдоторсионных углов (6), Uqq – кулоновских сил (7), Uvw – взаимодействий Ван-дер-Ваальса (8), UHb – водородных связей (9).
Для каждого типа взаимодействий вводится свой феноменологический закон.
Энергия валентных взаимодействий и энергия колебаний валентных углов описывается параболическими потенциалами (4), (5).
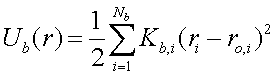(4)Kb,i – эффективная жёсткость валентной связи, i – номер связи в молекуле, Nb – полное число валентных связей, ri – длина связи, ro,i – равновесная длина связи.
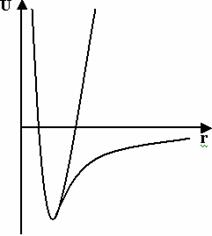
Рис. 1. Сравнение параболического и реального потенциалов для валентной связи. Параболическое представление потенциала делает возможным вести расчёт при высоких температурах без разрыва связи.
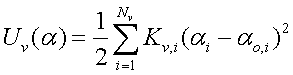(5)Kv,i – эффективная упругость валентного угла, i – номер валентного угла, Nv – полное число валентных углов, αi – значение валентного угла, αo,i – его равновесное значение.
Замена реального потенциала, описывающего валентные взаимодействия, на параболический (Рис. 1) оправдана тем, что при комнатных температурах колебания валентных связей малы. В то же время, в ряде задач необходимо проводить модельные расчёты при высоких температурах, и тогда использование параболического потенциала не приводит к разрыву валентных связей.
Потенциальная энергия для торсионных углов, плоских групп и псевдоторсионных углов задается общим выражением (6), представляющим собой ряд Фурье [3-5]. Было установлено, что во всех случаях достаточно оставлять не более четырёх членов ряда (включая нулевой).
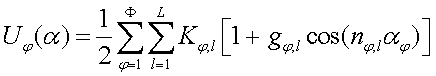(6)Kφ,l – константа, φ – номер торсионного угла, l – номер гармоники, gφ,l – вклад гармоники в потенциал торсионного угла (–1 < gφ,l < 1), nφ,l – кратность гармоники. Потенциалы Uf и Uφ отличаются константами.
Потенциальная энергия взаимодействия заряженных атомов характеризуется электростатическим потенциалом:
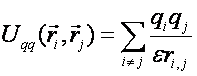(7)
, 
– координаты взаимодействующих атомов, qi, qj – их парциальные заряды, ε – диэлектрическая проницаемость среды (для вакуума ε = 1), 
.Взаимодействие между атомами, не связанными валентной связью, описываются с помощью потенциала Леннард-Джонса (8) или потенциала для водородной связи (9) [6].
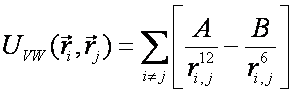(8)
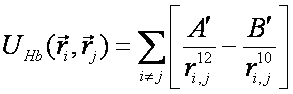(9)B и A, A' и B' – константы, определяющие глубину потенциальной ямы и расположение её минимума, 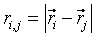, где , – координаты взаимодействующих атомов.
, где 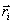, 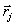– координаты взаимодействующих атомов.Отталкивание в этих формулах аппроксимируется членом ~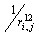 
, выбор степени 12 обусловлен математическими удобствами.
, выбор степени 12 обусловлен математическими удобствами.Водородная связь относится к специальному типу связи и обусловлена тем, что радиус иона H+ на порядок меньше, чем у других ионов. В формулах (8) и (9) имеется различие во вкладах, описывающих притяжение. Зависимость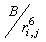 
в (8) соответствует дисперсионному диполь-дипольному взаимодействию, а 
в (9) вводится исходя из феноменологических соображений (Рис. 2). Отметим, что в ряде современных редакций силовых полей (например, AMBER, начиная с версии 96) потенциал водородных связей в форме (9) не используются, а эффективно учитывается комбинацией потенциалов Леннард-Джонса и кулоновских взаимодействий близлежащих атомов.
в (8) соответствует дисперсионному диполь-дипольному взаимодействию, а 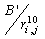в (9) вводится исходя из феноменологических соображений (Рис. 2). Отметим, что в ряде современных редакций силовых полей (например, AMBER, начиная с версии 96) потенциал водородных связей в форме (9) не используются, а эффективно учитывается комбинацией потенциалов Леннард-Джонса и кулоновских взаимодействий близлежащих атомов.
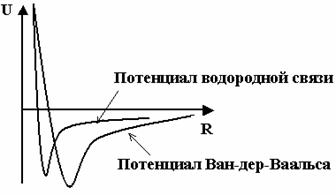
Рис. 2. Сравнение потенциалов для водородной связи и для взаимодействия Ван-дер-Ваальса.
Наиболее часто используемые силовые поля при расчётах био-макромолекулярных структур:
- AMBER (Assisted Model Building with Energy Refinement) используется для белков, нуклеиновых кислот и ряда других классов молекул. Не рекомендуется использовать для расчётов свойств материалов.
- CHARMm (Chemistry at HARvard Macromolecular mechanics) используется для различных систем от небольших молекул до сольватированных комплексов биологических макромолекул.
- CVFF (Consistent Valence Force Field) включает уточняющие вклады ангармоничности и взаимодействия составляющих силового поля. Поле параметризовано для расчётов пептидов и белков.
В программной реализации молекулярной динамики внутренние координаты системы пересчитываются в декартовы координаты атомов и, наоборот, с помощью алгоритма Эйринга.
