Молекулярная динамика белков и пептидов
Методическое пособие
1.4. Численное интегрирование. Метод Верле.
Существуют различные численные методы решения системы классических уравнений движения. В молекулярной динамике широко используется метод Верле [1], являющийся компромиссом между точностью процедуры и скоростью её реализации:
Силы, действующие на атом, находятся как производные потенциальной энергии:
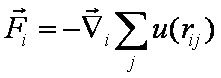 (19)
(19)Затем рассчитываются новые координаты атомов, из которых определяются равнодействующие силы:
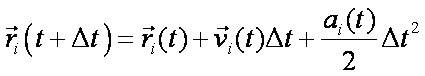 (20)
(20)Здесь a – ускорение, 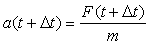 .
.
Далее определяются скорости атомов:
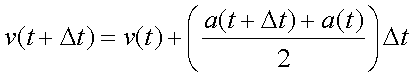 (21)
(21)Одной из наиболее существенных проблем процедуры интегрирования является выбор шага. При большом шаге погрешности интегрирования могут быть значительными, что приведёт к нестабильности траектории. При малом шаге существенно увеличивается время расчёта. В уравнениях движения, описывающих изменения по различным степеням свободы, временные характеристики существенно отличаются друг от друга. Для достаточно точного вычисления решения по быстрым и медленным переменным шаги интегрирования по ним могут различаться. По быстрым переменным может быть выбран значительно больший шаг [13]. В методе Верле шаг интегрирования берётся единым, оптимальным считается шаг 1 1,5 фс, что является примерно десятой частью периода самых быстрых молекулярных колебаний.
Начальные скорости атомов выбираются с помощью генератора случайных чисел в соответствии с распределением Максвелла при заданной температуре.