Молекулярная динамика белков и пептидов
Методическое пособие
2.2.2. Создание входных файлов для modyp.exe.
Структура молекулы, *.str
В этом файле содержатся данные о структуре и параметрах молекулы.
Section: HEAD Sequence: ACE-SER-NME, WAT, WAT, WAT, WAT, WAT, WAT Potential: amber96 Autor: Yaya. U. Date: 09-03-2003 Version: 1.12.1.1 Section: DATA vdwtype ER numbers absolute ............................................................................ ;Atom types atomtype C 12.0100 0.0860 3.8160 ;1 ............................................................................ ;Hydrogen bonds hbpair AB HW OW 0.02 0.03 ;1 ;Below molecule is placed molecule 1 M000001 residue 1 ACE atom HC +0.1123 2.17574 -0.85404 -3.17130 n 15 0.050 n 1H ;1 ............................................................................ write off atom H +0.2520 1.05174 -1.11504 -1.22430 n 15 0.050 n H ;8 atom CT +0.0350 0.25774 0.30496 0.15170 n 10 0.150 n CA ;9 write on ............................................................................ residue 2 SER atom N -0.4630 0.94874 -0.12604 -1.04630 n 09 0.180 n N ;7 ............................................................................ residue 3 NME atom N -0.4157 -0.86926 -0.61304 2.10170 n 09 0.180 n N ;18 ............................................................................ ;Valence bonds bond 1 2 340.000 1.090 ;1, HC-CT ............................................................................ ;Valence angles vang 1 2 3 35.000 109.500 ;1, HC-CT-HC ............................................................................ ;Torsion angles tang 6 5 2 1 0.800 0.0 1.0 next ;1, O-C-CT-HC tang 6 5 2 1 0.080 180.0 3.0 ;2, O-C-CT-HC ............................................................................ ;Out-of-plain (improper torsion) angles itang 2 7 5 6 10.500 180.0 2.0 ;1(57), CT-N-C-O ............................................................................ ;Sorry but EOF
SECTION: HEAD – раздел, содержащий следующую информацию:
AUTOR – имя создателя файла,
VERSION – версия программы PreMd,
SEQUENCE – последовательность остатков,
DATE – дата создания,
POTENTIAL – тип силового поля.
SECTION: DATA – раздел, содержащий информацию о типах атомов в молекуле и параметрах водородных и валентных связей, валентных углов, торсионных, а также псевдоторсионных углов:
VDWTYPE – тип выражения для потенциала:
AB 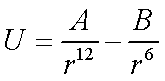 (27)
(27)
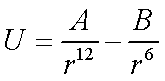 (27)
(27)ER 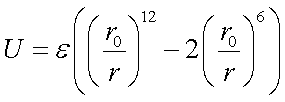 (28)
(28)
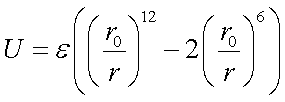 (28)
(28)ES 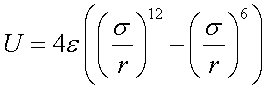 (29)
(29)
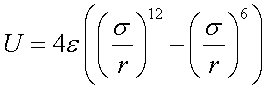 (29)
(29)NUMBERS – способ указания номеров:
| absolute | У всех атомов сквозная нумерация от первого до последнего |
| relative | Относительная нумерация |
| residue | Нумерация атомов внутри остатка |
| molecule | Нумерация атомов внутри молекулы |
MOLECULE:
| Номер молекулы | 1 |
| Название молекулы | M000001 |
RESIDUE:
| Номер остатка в молекуле | 1 |
| Название остатка | ACE |
ATOM – описание всех атомов в остатке:
| Тип атома | CT |
| Эффективный заряд | –0.3662 |
| Координаты по осям Х, Y и Z | 2.17574 0.23596 –3.17130 |
| Флаг фиксации атома во время счёта: n – атом не фиксируется, f – атом фиксируется | n |
| Код цвета атома 0–15 | 10 |
| Графический радиус атома, Å | 0.150 |
| Нужно ли отображать данный атом на экране: n – отображать, f – не отображать | n |
| Имя атома в остатке | CH3 |
| Комментарий | ;2 |
WRITE OFF – все атомы после данной строки и до строки WRITE ON не записываются в траекторный файл. По умолчанию эти строки отсутствуют, и все атомы записываются.
HBPAIR – настройка представления и параметров потенциала водородных связей в матрице парных взаимодействий атомов:
| Представление потенциала (30), (31), (32) | AB |
| Типы атомов | HW OW |
| Параметр А в выражении (30) или ε (31), (32) | 0.3 |
| Параметр В (30), r0 (31) или σ (32) | 0.8 |
| Комментарий | ;1 |
Выражения для используемых потенциалов:
AB 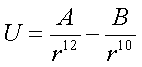 (30)
(30)
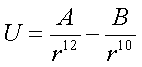 (30)
(30)ER 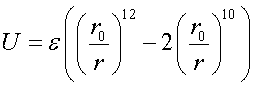 (31)
(31)
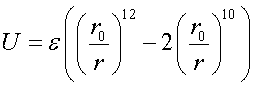 (31)
(31)ES 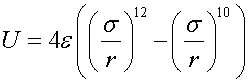 (32)
(32)
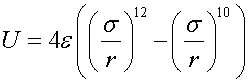 (32)
(32)VDWPAIR – настройка представления и параметров потенциала Ван-дер-Ваальса в матрице парных взаимодействий атомов:
| Представление потенциала (27), (28), (29) | AB |
| Типы атомов | СТ НС |
| Параметр А в выражении (27) или ε (28), (29) | 0.2 |
| Параметр В (27), r0 (31) или σ (29) | 3.5 |
| Комментарий | ;1 |
ATOMTYPE – типы атомов, встретившихся в молекуле:
| Тип атома | CT |
| Атомная масса | 12.0100 |
| Глубина потенциальной ямы для взаимодействий Ван-дер-Ваальса, ккал/моль | 0.1094 |
| Ван-дер-Ваальсов диаметр атома, Å (обратите внимание, что здесь стоит именно Ван-дер-Ваальсов диаметр атома, а не радиус, как в файле силового поля) | 3.8160 |
| После точки с запятой – комментарий, в данном случае – номер | ;1 |
BOND – описание всех связей в молекуле:
| Номера связанных атомов | 1 2 |
| Гармоническая силовая константа, ккал/моль·Å2 | 340.000 |
| Равновесная длина связи, Å | 1.090 |
| Номер связи | ;1 |
VANG – описание всех валентных углов:
| Номера атомов, образующих угол | 1 2 3 |
| Гармоническая силовая константа, ккал/моль·рад2 | 35.000 |
| Равновесное значение угла, градусы | 109.500 |
| Комментарий – номер угла и типы атомов | ;1, HC–CT–HC |
TANG – описание всех двугранных углов:
| Номера атомов, образующих угол | 6 5 2 1 | 6 5 2 1 |
| Высота барьера, ккал/моль | 0.15 | 26.60 |
| Сдвиг фазы, градусы | 180.0 | 180.0 |
| "Next" показывает, что в потенциале присутствует больше одной гармоники, параметры для неё берутся из следующей строки | Next | |
| Периодичность торсионного барьера | 1.0 | 3.0 |
| Комментарий – номер угла | ;1 | ;2 |
| Комментарий – типы атомов | O–C–CT–HC | O–C–CT–HC |
ITANG – описание всех псевдоторсионных углов:
| Номера атомов, образующих угол | 2 7 5 6 |
| Высота барьера, ккал/моль | 10.500 |
| Сдвиг фазы, градусы | 180. |
| Периодичность торсионного барьера | 2.0 |
| Комментарий – номер псевдоторсионного угла | ;1 |
| Комментарий – номер угла, начиная с торсионных | (57) |
| Комментарий – типы атомов | CT–N–C–O |
;SORRY BUT EOF – конец файла, без этой записи файл считается повреждённым.
Задание параметров *.prm
В файле *.prm содержатся данные обо всех параметрах, используемых при расчёте. Этот файл состоит из нескольких разделов. Через графический интерфейс программы MoDyp доступны не все из них. В данном файле все строки, начинающиеся с точки с запятой, содержат исключительно комментарии. Пустые строки не рассматриваются. Если строка не пустая, то она состоит из элементов, разделённых между собой символами (чаще всего – пробелами и табуляцией). Если первый элемент строки не отвечает ни одному ключевому слову, заданному в программе, то такая строка игнорируется. Ключевых слов всего четырнадцать, к ним относятся: Consts, Steps, Names, Calcprm, Termostat, Qmode, VDWmode, Hbmode, Flags, Periodic, Field_E, Field_G, RndGen, VLimit.
Создать параметрический файл можно в любом текстовом редакторе, задав расширение "prm", или через окно MoDyp: File –> New. Для редактирования уже существующего параметрического файла, нажать File –> Edit. Если файл уже создан, и никаких изменений в него вносить не требуется, достаточно нажать File –> Open.
;Parameters file ;Automaticly created by MoDypc Version: 1.13 build 1a section Mass Un. Angstrom psec Kbolts Eunits electron Consts 1 1 1 0.83144 418.4 372.704 section write graphic annotation Steps 100 1 10 section output tajectory structure file statistics batch Names Ephedrin.trj Ephedrin.str Ephedrin.tsb section Run Mode Max Tau Delta Tau Rvb(max) Graphical M Calcprm resume 100000 0.001 500 30 section Temperature Type Tau Freq. Mass Termostat 310 ber+col 0.5 55 18 section eps Rloff Q12 Q13 Q14 Qmode 1 20 0 0 1 section Rsoff W12 W13 W14 VDWmode 16 0 0 1 section Rhoff H12 H13 H14 HBmode 13 0 0 0 section pSx pSy pSz Periodic 100 100 100 section NoWr Cent Fix TNE WVel Flags 0 1 1 0 0 ;Sorry but EOF
Разделы файла *.prm:
1. Раздел Consts.
Этот раздел не доступен через графический интерфейс программы MoDyp. Он создаётся автоматически при создании файла *.prm.
В программе MoDyp используется система единиц "ДАПС" (от "Дальтон", "Ангстрем", "пикосекунда"). Раздел Consts (константы) определяет настройку системы единиц. Все единицы, используемые в нужной системе единиц (СИ, СГС и др.), должны быть выражены через стандартные (Да, A, пс). Все числа имеют формат "с плавающей точкой", степень записывается при помощи буквы "е", далее следуют "минус" или "плюс" (может быть опущен). Учитываются 10 знаков после запятой.
| Раздел | section | Consts |
| Единица массы (Да) | Mass Un. | 1 |
| Ангстрем | Angstrom | 1 |
| Пикосекунда | psec | 1 |
| Постоянная Больцмана | Kbolts | 0.83144 |
| Единица энергии (ккал/моль) | Eunits | 418.4 |
| Заряд электрона | electron | 372.704 |
2. Раздел Steps
В данном разделе указывается число шагов интегрирования, через которое необходимо произвести запись в траекторный файл, обновить изображение на экране и записать информацию в файл аннотации (Рис. 11).
| Раздел | section | Steps |
| Частота записи в траекторный файл (в шагах интегрирования) | write | 100 |
| Частота обновления изображения на экране | graphic | 1 |
| Частота записи в файл аннотации | annotation | 10 |
Информацию, относящуюся к данному разделу можно также заполнить через окно редактора MoDyp: File –> New. Для редактирования уже существующего параметрического файла, нажать File –> Edit.
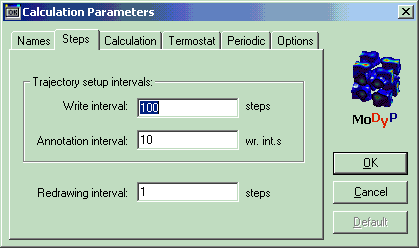
Рис. 10. Раздел Steps в графическом интерфейсе программы. Write interval – частота записи в траекторный файл, Annotation interval – частота записи в файл аннотации, Redrawing interval – частота обновления изображения на экране.
3. Раздел Names
В этом разделе указываются имена файлов, которые будут использованы при расчёте. Их всего три – траекторный файл, куда будет записываться вся информация в ходе расчёта; файл, содержащий структуру молекулы и данные о параметрах потенциального поля (*.str) и файл, в котором указано, какие типы статистик необходимо получить в процессе расчёта (*.tsb).
| Раздел | section | Names |
| Название траекторного файла | output tajectory | Ephedrin.trj |
| Название файла со структурой молекулы | structure file | Ephedrin.str |
| Название файла со статистиками | statistics batch | Ephedrin.tsb |
В окне редактора MoDyp (раздел Names) можно написать имена новых файлов или открыть уже существующие, нажав на клавишу ":". Нужно обратить внимание, что при использовании клавиши ":", в параметрический файл заносится полный путь к файлу. Это необходимо, если запуск программы MoDyp осуществляется не из директории с рассчитываемой молекулой. Однако удобнее переписывать файл modyp.exe в нужную директорию, и осуществлять запуск оттуда. В этом случае указывать полный путь к файлам нецелесообразно (лучше оставлять только имена без указания пути), так как при переносе счёта на другой компьютер, пути к файлам могут быть другими, и продолжение счёта окажется невозможным.
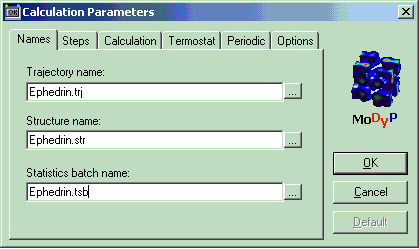
Рис. 11 Раздел Names в графическом интерфейсе программы. Trajectory name – название траекторного файла, Structure name – название файла со структурой и параметрами силового поля, Statistic batch name – название файла со статистиками.
4. Раздел Calcprm
Здесь содержится информация о параметрах расчёта:
| Раздел | section | Calcprm | |
| Режим счёта | Run Mode | Релаксация | relaxation |
| Начало расчёта, начальные скорости равны нулю | start | ||
| Начало расчёта, начальные скорости разыгрываются в соответствии с распределением Максвелла | vstart | ||
| Продолжение траектории | resume | ||
| Продолжение траектории, скорости равны нулю | vresume | ||
| Максимальное время интегрирования, пс | Max Tau | "Длина траектории" | 100000 |
| Шаг интегрирования, пс | Delta Tau | 0.001 | |
| Размер ячейки с абсолютно отражающими стенками | Rvb(max) | Здесь – диаметр сферической ячейки | 500 |
| Графический масштаб | Graphical M | Число пикселей на 1Å | 30 |
Обычно перед расчётом проводят релаксацию молекулы. Это необходимо для того, чтобы избежать разрушения молекулы вследствие дефектов при её построении. В молекулярных редакторах не всегда точно соблюдаются расстояния между атомами. Два атома могут оказаться расположенными слишком близко друг к другу. Так, в программе HyperChem часто к PDB-структуре, полученной методами, которые не позволяют определить координаты атомов водорода, добавляются эти атомы. Если атомы оказываются расположенными слишком близко, энергия резко возрастает. Чтобы избежать этого, в начале процесса релаксации Ван-дер-Ваальсовы радиусы атомов берутся минимальными. В процессе релаксации они увеличиваются до стандартного размера, а диэлектрическая проницаемость среды уменьшается от до заданной. Релаксацию проводят обычно на временах 10-50 пс.
Если молекула уже находится в минимуме энергии, и релаксация не требуется, используются два режима – start или vstart.
После релаксации продолжение траектории осуществляется с помощью режимов resume или vresume.
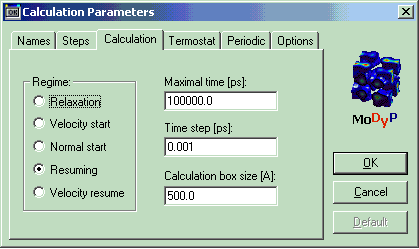
Рис. 12. Раздел Calculation в графическом интерфейсе программы. Regime – режим счёта, Maximal time – время счёта ("длина траектории") в пс, Time step – шаг интегрирования в пс, Calculation box size – размер ячейки с абсолютно отражающими стенками в Å.
5. Раздел Termostat.
| Раздел | section | Termostat | |
| Температура | Temperature | Обычно 300 – 2000 К | 310 |
| Тип термостата | Type | Нет термостата (режим исполь-зуется, чтобы задать расчёт только со столкновительным термостатом) | none |
| Столкновительный термостат | col | ||
| Термостат Берендсена | ber | ||
| Постоянное число частиц, объём и температура | nvt | ||
| Постоянное число частиц, объём и давление | nvp | ||
| Можно использовать сразу два типа | ber+col | ||
| Характерное время изменения скорости атома, пс | Tau | Для термостата Берендсена. Нужно задавать эту величину, даже если термостат Берендсена не используется! | 0.5 |
| Частота столкновений, пс–1 | Freq. | Для столкновительного термостата – частота столкновений виртуальных частиц с атомами рассчитываемой системы | 55 |
| Масса виртуальной частицы, аем | Mass | Для столкновительного термостата | 18 |
Термостаты позволяют поддерживать заданную температуру рассчитываемой системы. Стандартной считается температура 300 К. Для более полного сканирования энергетической поверхности используют расчёты при высоких температурах (обычно 2000 К). В программе MoDyp возможно использование коллизионного термостата вместе с термостатами NVT, NVE и Берендсена.
Если производится расчёт молекулы в вакууме, и используется столкновительный термостат, то для имитации водного окружения частоту столкновений задают равной 55 – 60 пс–1, а массу виртуальных частиц 18 аем. Если рассчитывается молекула в воде, столкновения задают более частыми (около 100 пс–1), масса виртуальных частиц при этом должна быть небольшой (0.1 аем).
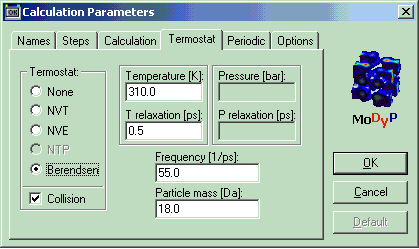
Рис. 13. Раздел Termostat в графическом интерфейсе программы. Termostat – тип термостата. Чтобы использовать только столкновительный термостат, нужно выбрать none и Collision. Temperature – температура в К, T relaxation – характерное время изменения скорости атомов в термостате Берендсена в пс, Frequency – частота столкновений в пс–1, Particle mass – масса виртуальной частицы в аем.
6. Раздел Qmode
Контроль над расчётом кулоновских взаимодействий. Возможен только в текстовом режиме.
| Раздел | section | Qmode | |
| Диэлектрическая проницаемость среды | eps | 1 | |
| Радиус обрезания, Å | Rloff | Расстояние, на котором перестают действовать кулоновские силы | 20 |
| 1–2 взаимодействие | Q12 | 0 | |
| 1–3 взаимодействие | Q13 | 0 | |
| 1–4 взаимодействие | Q14 | 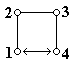 |
1 |
7. Раздел VdWmode
Контроль над расчётом взаимодействий Ван-дер-Ваальса. Возможен только в текстовом режиме.
| Раздел | section | VdWmode | |
| Радиус обрезания, Å | Rsoff | Расстояние, на котором перестают действовать силы Ван-дер-Ваальса; обычно составляет 80% от радиуса обрезания для кулоновских сил | 16 |
| 1–2 взаимодействие | W12 | 0 | |
| 1–3 взаимодействие | W13 | 0 | |
| 1–4 взаимодействие | W14 |  |
1 |
8. Раздел HBmode
Контроль над расчётом водородных взаимодействий. Возможен только в текстовом режиме.
| Раздел | section | HBmode | |
| Радиус обрезания, Å | Rhoff | Расстояние, на котором перестают действовать водородные взаимодействия; обычно составляет 65% от радиуса обрезания для кулоновских сил | 16 |
| 1–2 взаимодействие | H12 | 0 | |
| 1–3 взаимодействие | H13 | 0 | |
| 1–3 взаимодействие | H14 |  Для лёгкоатомных моделей H14 = 0, для полноатомных H14=1 Для лёгкоатомных моделей H14 = 0, для полноатомных H14=1 |
0 |
9. Раздел Options.
В окне программы MoDyp (через графический интерфейс) этот раздел называется "Options". В него помимо раздела "Flags" (выделенного в отдельный раздел) входят три других параметра. Это – диэлектрическая проницаемость среды (раздел "Qmode" в текстовом режиме), графический масштаб, число пикселей на ангстрем при выводе на экран (раздел "Calcprm") и радиус обрезания кулоновских взаимодействий (раздел "Qmode"). Через графический режим нельзя задать отдельные значения для радиусов обрезания для взаимодействий Ван-дер-Ваальса и для водородных связей, они принимаются равными 80% и 65% от радиуса обрезания кулоновских взаимодействий соответственно.
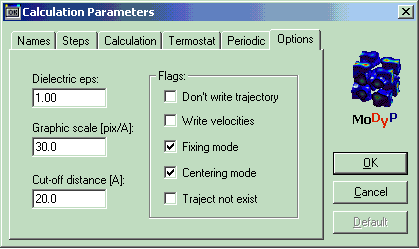
Рис. 14. Раздел Options в графическом интерфейсе программы. Dielectric eps – диэлектрическая проницаемость среды. Graphic scale [pix/A] – графический масштаб, пикс/Å (какое количество пикселей занимает один ангстрем при выводе на экран). Cut-off distance [A] – радиус обрезания электростатических для взаимодействий, Å.
| Раздел | section | Flags | |
| Запись траектории в файл | NoWr | Нужно ответить на вопрос: "Не записывать траекторию?" 0 – записывать, 1 – не записывать (не будут создаваться файлы trj и ann) | 0 |
| Центрирование при выводе на экран | Сent | Не влияет на координаты атомов | 1 |
| Фиксация | Fix | 1 – фиксировать, 0 – не фиксировать |
0 |
| Траектории не существует | TNE | При использовании опций resume и vresume (продолжение счёта), если раньше (например, при релаксации) траектория не создавалась | 0 |
| Запись скоростей | Wvel | В файл trj записываются не координаты, а скорости атомов (1). | 0 |
Фиксация атомов задаётся в файле str (секция "ATOM", колонка, идущая после координат атома). Помеченные в str атомы фиксируются, если параметр Fix равен единице. Если в файле str некоторые атомы заданы, как фиксируемые, а фиксация запрещена (Fix = 0), то такие атомы будут отражаться от абсолютно упругих стенок периодической решётки.
10. Раздел Periodic.
При расчётах нескольких молекул необходимо использовать периодические граничные условия. Так, при расчёте аминокислотного остатка в воде обычно используется решётка с длиной ребра 20 Å. Это необходимо, чтобы поддерживать плотность молекул. Без периодических граничных условий при расчёте нескольких молекул, эти молекулы будут стремиться как можно дальше разлететься друг от друга. Если используются периодические условия, то атом, вылетающий за его границы, оказывается с противоположной стороны ячейки.
Рис. 15. Раздел Periodic в графическом интерфейсе программы. X, Y, Z dimention – периодические граничные условия по осям X, Y и Z. X, Y, Z size [A] – размер ребра решётки по осям X, Y, Z в Å.
| Раздел | section | Periodic | |
| Размер по оси X, Å | pSx | При расчёте молекулы в водной среде, задают периодическую решётку такого размера, какой был задан в HyperChem | 100 |
| Размер по оси Y, Å | pSy | 100 | |
| Размер по оси Z, Å | pSz | 100 |
Задание статистик *.tsb
Файл со статистиками можно создать в текстовом редакторе, либо через окно программы MoDyp. Если статистики задаются в текстовом редакторе, то необходимо дописать и служебную информацию, без которой запуск MoDyp невозможен. При использовании MoDyp для создания такого файла, эта информация записывается автоматически:
;Statistics batch file ;Automaticly created by Modyp Version: 1.13 build 1a tAdvanced 10 adv.dat tmaxwell 200 100,000,150 "maxwell" maxwell.dat tDistCf 1 2 1 2 10 60.000 128,000,000 "distcf" distcf.dat tCrossCf 1 2 10 50.000 128,000,255 "crosscf" crosscf.dat tAutoCfd 1 10 70.000 128,000,128 "autocfd" autocfd.dat tAutoCf 1 10 70.000 000,255,064 "autocf" autocf.dat tProb3D 1 2 3 30 "prob3d" prob3d.dat tProb2D 41 3 90 255,128,000 "prob2d" prob2d.dat tProbDb 21 200 000,255,255 "probdb" probdb.dat tDistDb 1 2 200 000,000,000 "distdb" distdb.dat tDistDevCf 1 2 4 6 10 100.000 000,000,000 "DistDevCf" tDistDevCf.dat tDist2AixCf 1 4 7 9 10 100.000 000,000,000 "Dist2AixCf" tDist2AixCf.dat ;Sorry but EOF
Чтобы создать файл со статистиками через окно Modyp, нужно вызвать MoDyp*.exe, затем нажать: File –> Edit –> выбрать нужный prm – файл (если его нет, то перед заданием статистик, нужно создать его!) –> открыть –> ОК. С помощью этой последовательности команд, MoDyp считывает нужную информацию и даёт возможность создать файл со статистиками: File –> Statistics –> New.
Для создания любой из статистик нужно выбрать номер статистики.
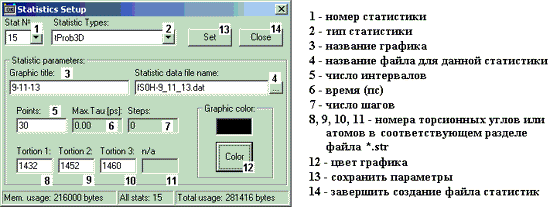
Рис. 16. Окно создания статистик. Для создания любой из статистик нужно выбрать её номер (1), задать тип статистики (2), указать название графика (3) – оно должно начинаться с буквы (лучше латинского алфавита) и быть более двух символов, внести все параметры в активные для выбранного типа статистики окна (4-11), выбрать цвет графика (12) – по умолчанию цвет чёрный, выбранный цвет будет использоваться только программой MoDyp во время счёта. После создания статистики необходимо нажать set (13)! После создания и сохранения всех статистик – close (14).
Во время счёта MoDyp позволяет рассчитывать двенадцать типов статистик.
1. tAdvanced
В файл данной статистики записываются текущие и средние значения энергий различных типов взаимодействий (ккал/моль), дипольного момента молекулы (Дебай), температуры. Эту статистику необходимо задавать для любого расчёта. Если задана эта статистика, то все значения через определённое количество шагов заносятся в так называемый "файл аннотации" – файл с расширением ann.
| Номер параметра (см. Рис. 16) | Название параметра | Наиболее часто используемое значение | Примечание |
| 4 | Название файла для данной статистики | Adv.dat | Задать любое имя файла, воспользовавшись строкой ввода, указав расширение – dat, или нажать на "...", выбрав нужную директорию. По умолчанию файлы со статистиками записываются в директорию, из которой произведён запуск MoDyp |
| 10 | Число шагов | 10 | Через указанное количество шагов интегрирования вычисляется дисперсия (d, см. табл. 4), и происходит усреднение |
| 13 | Сохранить параметры | Нужно обязательно нажать, после внесения всех параметров, иначе их невозможно будет восстановить! |
При задании статистики в текстовом режиме:
| Тип статистики | tAdvanced |
| Число шагов | 10 |
| Название файла для данной статистики | adv.dat |
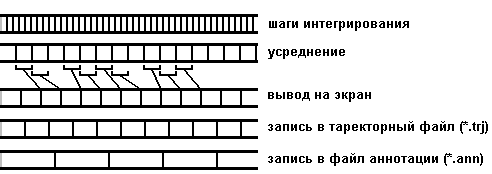
Рис. 17. Усреднение данных, полученных путём интегрирования уравнений движения.
Таблица 4. Выходной файл для расширенной статистики tAdvanced. Time – время в пс и шагах интегрирования; c – текущее значение параметра, а – среднее, d – дисперси.
tAdvanced statistic type Time: 50.001 psec Step: 50001 Averaging factor (steps): 50002 Temperature: c=284.11 K a=176.01 K d=6413.73 K^2 Bonded energy: c=7.45 kcal/mol a=5.054 kcal/mol d=7.112 (kcal/mol)^2 Valence energy: c=7.294 kcal/mol a=6.627 kcal/mol d=8.907 (kcal/mol)^2 Tortion energy: c=3.551 kcal/mol a=2.661 kcal/mol d=2.182 (kcal/mol)^2 Qulombic energy: c=0.000 kcal/mol a=0.000 kcal/mol d=0.000 (kcal/mol)^2 Van-der-Waalse energy: c=11.113 kcal/mol a=-0.354 kcal/mol d=6.979 (kcal/mol)^2 Hydrogen bonds energy: c=0.000 kcal/mol a=0.000 kcal/mol d=0.000 (kcal/mol)^2 Kinetic energy: c=22.866 kcal/mol a=14.165 kcal/mol d=41.543 (kcal/mol)^2 Potential energy: c=29.410 kcal/mol a=13.987 kcal/mol d=53.947 (kcal/mol)^2 Dipole moment (abs.): c=0.000e+000 e*A a=0.000e+000 e*A d=0.000e+000 (e*A)^2 Dipole moment (comp.): x=0.00e+000 e*A y=0.00e+000 e*A z=0.00e+000 e*A ;Sorry but EOF
2. tMaxwell
Данный тип статистики выводит информацию о распределении атомов по скоростям, что позволяет судить о правильности получаемых результатов. Если кривая, выводящаяся на экране, имеет нестандартный для распределения Максвелла вид, то необходимо устранить все ошибки, приводящие к некорректным результатам. На начальном этапе счёта (до 100 пс) обычно происходит оптимизация скоростей молекул, график может исчезать и появляться снова, так как происходит обнуление данных, если скорость атома в 1,2 раза превышает скорость на предыдущем шаге.
| Номер параметра (см. Рис. 16) | Название параметра | Наиболее часто используемое значение | Примечание |
| 3 | Название графика | Maxwell | Любое имя, которое начинается с латинской буквы и имеет длину более двух символов. Имя будет использоваться не только при расчёте, но и при построении графиков с помощью программного пакета Matlab |
| 4 | Название файла для данной статистики | Max.dat | Задать любое имя файла, которое ранее не было использовано для другой статистики! |
| 5 | Число интервалов | 200 | Количество интервалов, на которое разбивается диапазон скоростей атомов |
| 12 | Цвет | 000,000,000 | Используется стандартная RGB – палитра (красный, зелёный, синий). По умолчанию цвет чёрный. Белый: 256, 256, 256. Серый: три одинаковые цифры. Красный: 256,000,000 |
При задании статистики в текстовом режиме:
| Тип статистики | tmaxwell |
| Число интервалов | 200 |
| Цвет | 100,000,150 |
| Название графика (обязательно в кавычках) | "maxwell" |
| Название файла для данной статистики | maxwell.dat |
Таблица 5. Выходной файл для статистики tMaxwell. Velocity – скорости атомов (число строк соответствует числу заданных интервалов), probability – вероятность того, что скорость атома попадает в интервал скоростей.(vi, vi+1).
Modyp 1.13 build 1a Statistics data file. Data for <Maxwell> tMaxwell statistic type Velocity Probability +0000.0000 2.6642e-004 +0001.0025 1.6954e-003 +0002.0050 4.5335e-003 +0003.0075 8.3471e-003 ... ... +0049.1219 1.1009e-005 ;Sorry but EOF
3. tDistDb
Статистика DistDb позволяет получить распределение по расстоянию между двумя атомами.
| Номер параметра (см. Рис. 16) | Название параметра | Наиболее часто используемое значение | Примечание |
| 3 | Название графика | Любое имя, которое начинается с латинской буквы и имеет длину более двух символов. Имя будет использоваться не только при расчёте, но и при построении графиков с помощью программного пакета Matlab | |
| 4 | Название файла для данной статистики | Задать любое имя файла, которое ранее не было использовано для другой статистики! | |
| 5 | Число интервалов | 200 | Количество интервалов, на которое разбивается диапазон скоростей атомов |
| 8 | Номер первого атома | Номера атомов можно узнать в файле *.str по номеру комментария в строке нужного атома | |
| 9 | Номер второго атома | ||
| 12 | Цвет | Используется стандартная RGB – палитра (красный, зелёный, синий). По умолчанию цвет чёрный. Белый: 256, 256, 256. Серый: три одинаковые цифры. Красный: 256,000,000 |
При задании статистики в текстовом режиме:
| Тип статистики | tDistDb |
| Номер первого атома | 1 |
| Номер второго атома | 12 |
| Число интервалов | 200 |
| Цвет | 000,000,255 |
| Название графика (обязательно в кавычках) | "DistDb" |
| Название файла для данной статистики | DistDb.dat |
Таблица 6. Выходной файл для статистики tDistDb. Distance – расстояние между атомами (число строк соответствует числу заданных интервалов), probability – вероятность того, что расстояние между атомами попадает в интервал (di, di+1).
Modyp 1.13 build 1a Statistics data file. Data for <DistDb> tDistDb statistic type Distance Probability +0005.2198 4.5493e+002 +0005.2287 1.4785e+003 +0005.2375 2.1609e+003 +0005.2463 1.9334e+003 ... ... +0006.9783 1.7060e+003 ;Sorry but EOF
4. tProbDb
Одномерное распределение плотности вероятности по торсионному углу.
| Номер параметра (см. Рис. 16) | Название параметра | Наиболее часто используемое значение | Примечание |
| 3 | Название графика | Любое имя, которое начинается с латинской буквы и имеет длину более двух символов. Имя будет использоваться не только при расчёте, но и при построении графиков с помощью программного пакета Matlab | |
| 4 | Название файла для данной статистики | Задать любое имя файла, которое ранее не было использовано для другой статистики! | |
| 5 | Число интервалов | 200 | Количество интервалов, на которое разбивается диапазон от –180 до +180 градусов |
| 8 | Номер торсионного угла | Номер угла можно узнать в файле *.str по номеру комментария в строке нужного угла | |
| 12 | Цвет | Используется стандартная RGB – палитра (красный, зелёный, синий). По умолчанию цвет чёрный. Белый: 256, 256, 256. Серый: три одинаковые цифры. Красный: 256,000,000 |
При задании статистики в текстовом режиме:
| Тип статистики | tProbDb |
| Номер торсионного атома | 9 |
| Число интервалов | 200 |
| Цвет | 255,255,000 |
| Название графика (обязательно в кавычках) | "ProbDb" |
| Название файла для данной статистики | ProbDb.dat |
Таблица 7. Выходной файл для статистики tProbDb. Angle – значение торсионного угла, probability – вероятность того, что значение угла попадает в интервал (φi, φi+1).
Modyp 1.13 build 1a Statistics data file. Data for <ProbDb> tProbDb statistic type Angle Probability -180.00 3.3332e-005 -178.20 2.8888e-004 -176.40 6.7775e-004 ... ... +178.20 4.8098e-002 ;Sorry but EOF
5. tProb2D
Двумерное распределение плотности вероятности по торсионным углам.
| Номер параметра (см. Рис. 16) | Название параметра | Наиболее часто используемое значение | Примечание |
| 3 | Название графика | Любое имя, которое начинается с латинской буквы и имеет длину более двух символов. Имя будет использоваться не только при расчёте, но и при построении графиков с помощью программного пакета Matlab | |
| 4 | Название файла для данной статистики | Задать любое имя файла, которое ранее не было использовано для другой статистики! | |
| 5 | Число интервалов | 90 | Количество интервалов, на которое разбивается диапазон от –180 до +180 градусов |
| 8 | Номер первого торсионного угла | Номер угла можно узнать в файле *.str по номеру комментария в строке нужного угла | |
| 9 | Номер второго торсионного угла | ||
| 12 | Цвет | 000,000,000 | Используется стандартная RGB – палитра (красный, зелёный, синий). По умолчанию цвет чёрный. Белый: 256, 256, 256. Серый: три одинаковые цифры. Красный: 256,000,000 |
При задании статистики в текстовом режиме:
| Тип статистики | tProb2D |
| Номер первого торсионного угла | 10 |
| Номер второго торсионного угла | 14 |
| Число интервалов | 90 |
| Цвет | 255,255,000 |
| Название графика (обязательно в кавычках) | "Prob2D" |
| Название файла для данной статистики | Prob2D.dat |
Таблица 8. Выходной файл для статистики tProb2D. Angle1, angle2 – значения торсионных углов, probability – вероятность того, что значение угла попадает в интервал (φi, φi+1).
Modyp 1.13 build 1a Statistics data file. Data for <Prob2D> tProb2D statistic type Angle1 Angle2 Probability -180.00 -180.00 5.8474e-003 -176.00 -180.00 2.2050e-003 -172.00 -180.00 6.9249e-004 ... ... ... +176.00 +176.00 5.9224e-003 ;Sorry but EOF
6. tProb3D
Трёхмерное распределение плотности вероятности по торсионным углам.
| Номер параметра (см. Рис. 16) | Название параметра | Наиболее часто используемое значение | Примечание |
| 3 | Название графика | Любое имя, которое начинается с латинской буквы и имеет длину более двух символов. Имя будет использоваться не только при расчёте, но и при построении графиков с помощью программного пакета Matlab | |
| 4 | Название файла для данной статистики | Задать любое имя файла, которое ранее не было использовано для другой статистики! | |
| 5 | Число интервалов | 30 | Количество интервалов, на которое разбивается диапазон от –180 до +180 градусов |
| 8 | Номер первого торсионного угла | Номер угла можно узнать в файле *.str по номеру комментария в строке нужного угла | |
| 9 | Номер второго торсионного угла | ||
| 10 | Номер второго торсионного угла |
При задании статистики в текстовом режиме:
| Тип статистики | tProb3D |
| Номер первого торсионного угла | 2 |
| Номер второго торсионного угла | 5 |
| Номер третьего торсионного угла | 18 |
| Число интервалов | 30 |
| Название графика (обязательно в кавычках) | "Prob3D" |
| Название файла для данной статистики | Prob3D.dat |
Таблица 9. Выходной файл для статистики tProb3D. Angle1, angle2, angle3 – значения торсионных углов, probability – вероятность того, что значение угла попадает в интервал (φi, φi+1).
Modyp 1.13 build 1a Statistics data file. Data for <Prod3D> tProb3D statistic type Angle1 Angle2 Angle3 Probability -180.00 -180.00 -180.00 3.2456e-007 -180.00 -180.00 -168.00 3.5245e-005 -180.00 -180.00 -156.00 5.2422e-005 ... ... ... ... -168.00 -180.00 -168.00 5.7933e-007 -168.00 -180.00 -156.00 2.6309e-006 -168.00 -180.00 -144.00 8.9278e-005 ... ... ... ... +144.00 -180.00 -168.00 9.9500e-007 +144.00 -180.00 -156.00 2.3101e-008 +144.00 -180.00 -144.00 1.1611e-007 ... ... ... ... -180.00 -168.00 -180.00 1.7112e-006 -180.00 -168.00 -168.00 7.0613e-007 -180.00 -168.00 -156.00 1.4732e-006 ... ... ... ... +168.00 +168.00 +168.00 1.6514e-006 ;Sorry but EOF
7. tAutoCf
Ненормированная автокорреляционная функция для торсионного угла.
| Номер параметра (см. Рис. 16) | Название параметра | Наиболее часто используемое значение | Примечание |
| 3 | Название графика | Любое имя, которое начинается с латинской буквы и имеет длину более двух символов. Имя будет использоваться не только при расчёте, но и при построении графиков с помощью программного пакета Matlab | |
| 4 | Название файла для данной статистики | Задать любое имя файла, которое ранее не было использовано для другой статистики! | |
| 6 | Время корреляции, пс | 70 | Время наблюдения корреляции на протяжении всей траектории |
| 7 | Число шагов | 10 | Число шагов интегрирования, через которое обновляются данные о корреляции |
| 8 | Номер торсионного угла | Номер угла можно узнать в файле *.str по номеру комментария в строке нужного угла |
При задании статистики в текстовом режиме:
| Тип статистики | tAutoCf |
| Номер торсионного угла | 1 |
| Число шагов | 10 |
| Время корреляции, пс | 70 |
| Цвет | 000,255,064 |
| Название графика (обязательно в кавычках) | "AutoCf" |
| Название файла для данной статистики | AutoCf.dat |
Таблица 10. Выходной файл для статистики tAutoCf. Time – время, Real part of aCorr function – значение действительной части автокорреляционной функции.
Modyp 1.13 build 1a Statistics data file. Data for <AutoCf> tAutoCf statistic type Time Real part of aCorr function +0000.0000 1.0000e+000 +0000.0100 9.7219e-001 ... ... +0069.9900 9.1925e-001 ;Sorry but EOF
8. tAutoCfD
Нормированная автокорреляционная функция для торсионного угла.
| Номер параметра (см. Рис. 16) | Название параметра | Наиболее часто используемое значение | Примечание |
| 3 | Название графика | Любое имя, которое начинается с латинской буквы и имеет длину более двух символов. Имя будет использоваться не только при расчёте, но и при построении графиков с помощью программного пакета Matlab | |
| 4 | Название файла для данной статистики | Задать любое имя файла, которое ранее не было использовано для другой статистики! | |
| 6 | Время корреляции, пс | 70 | Время наблюдения корреляции на протяжении всей траектории |
| 7 | Число шагов | 10 | Число шагов интегрирования, через которое обновляются данные о корреляции |
| 8 | Номер торсионного угла | Номер угла можно узнать в файле *.str по номеру комментария в строке нужного угла |
При задании статистики в текстовом режиме:
| Тип статистики | tAutoCfD |
| Номер торсионного угла | 1 |
| Число шагов | 10 |
| Время корреляции, пс | 70 |
| Цвет | 128,000,128 |
| Название графика (обязательно в кавычках) | "AutoCfD" |
| Название файла для данной статистики | AutoCfD.dat |
Таблица 11. Выходной файл для статистики tAutoCfD. Time – время, Real part of aCorr function – значение действительной части автокорреляционной функции.
Modyp 1.13 build 1a Statistics data file. Data for <AutoCfD> tAutoCfD statistic type Time Real part of aCorr function +0000.0000 0.0000e+000 +0000.0050 1.5839e-001 ... ... +0069.9950 3.6205e-001 ;Sorry but EOF
9. tCrossCf
Кросскорреляционная функция для торсионного угла.
| Номер параметра (см. Рис. 16) | Название параметра | Наиболее часто используемое значение | Примечание |
| 3 | Название графика | Любое имя, которое начинается с латинской буквы и имеет длину более двух символов. Имя будет использоваться не только при расчёте, но и при построении графиков с помощью программного пакета Matlab | |
| 4 | Название файла для данной статистики | Задать любое имя файла, которое ранее не было использовано для другой статистики! | |
| 6 | Время корреляции, пс | 50 | Время наблюдения корреляции на протяжении всей траектории |
| 7 | Число шагов | 10 | Число шагов интегрирования, через которое обновляются данные о корреляции |
| 8 | Номер первого торсионного угла | Номер угла можно узнать в файле *.str по номеру комментария в строке нужного угла | |
| 9 | Номер второго торсионного угла |
При задании статистики в текстовом режиме:
| Тип статистики | tCrossCf |
| Номер первого торсионного угла | 1 |
| Номер второго торсионного угла | 2 |
| Число шагов | 10 |
| Время корреляции, пс | 70 |
| Цвет | 128,000,255 |
| Название графика (обязательно в кавычках) | "CrossCf" |
| Название файла для данной статистики | CrossCf.dat |
Таблица 12. Выходной файл для статистики tCrossCf. Time – время, Real part of сCorr function – значение действительной части кросскорреляционной функции.
Modyp 1.13 build 1a Statistics data file. Data for <CrossCf> tCrossCf statistic type Time Real part of cCorr function +0000.0000 0.0000e+000 +0000.0080 2.9416e-002 ... ... +0049.9920 2.8687e-002 ;Sorry but EOF
10. tDistCf
Авто- или кросскорреляционная функция расстояния между атомами.
| Номер параметра (см. Рис. 16) | Название параметра | Наиболее часто используемое значение | Примечание |
| 3 | Название графика | Любое имя, которое начинается с латинской буквы и имеет длину более двух символов. Имя будет использоваться не только при расчёте, но и при построении графиков с помощью программного пакета Matlab | |
| 4 | Название файла для данной статистики | Задать любое имя файла, которое ранее не было использовано для другой статистики! | |
| 6 | Время корреляции, пс | 60 | Время наблюдения корреляции на протяжении всей траектории |
| 7 | Число шагов | 10 | Число шагов интегрирования, через которое обновляются данные о корреляции |
| 8 | Номер первого атома | Номер угла можно узнать в файле *.str по номеру комментария в строке нужного угла | |
| 9 | Номер второго атома | ||
| 10 | Номер третьего атома | Для автокорреляционной функции номер должен совпадать с номером первого атома | |
| 11 | Номер четвёртого атома | Для автокорреляционной функции номер должен совпадать с номером второго атома |
При задании статистики в текстовом режиме (пример для автокорреляционной функции):
| Тип статистики | tDistCf |
| Номер первого торсионного угла | 1 |
| Номер второго торсионного угла | 2 |
| Номер третьего торсионного угла | 1 |
| Номер четвёртого торсионного угла | 2 |
| Число шагов | 10 |
| Время корреляции, пс | 60 |
| Цвет | 128,000,000 |
| Название графика (обязательно в кавычках) | "DistCf" |
| Название файла для данной статистики | DistCf.dat |
Таблица 13. Выходной файл для статистики tDistCf. Time – время, Corr function – значение корреляционной функции.
Modyp 1.13 build 1a Statistics data file. Data for <DistCf> tDistCf statistic type Time Corr function +0000.0000 2.0047e+000 +0000.0100 2.0047e+000 ... ... +0059.9900 2.0075e+000 ;Sorry but EOF
11. tDistDevCf
Корреляционная функция отклонения от среднего:
| Номер параметра (см. Рис. 16) | Название параметра | Наиболее часто используемое значение | Примечание |
| 3 | Название графика | Любое имя, которое начинается с латинской буквы и имеет длину более двух символов. Имя будет использоваться не только при расчёте, но и при построении графиков с помощью программного пакета Matlab | |
| 4 | Название файла для данной статистики | Задать любое имя файла, которое ранее не было использовано для другой статистики! | |
| 6 | Время корреляции, пс | 100 | Время наблюдения корреляции на протяжении всей траектории |
| 7 | Число шагов | 10 | Число шагов интегрирования, через которое обновляются данные о корреляции |
| 8 | Номер первого атома | Номер угла можно узнать в файле *.str по номеру комментария в строке нужного угла | |
| 9 | Номер второго атома | ||
| 10 | Номер третьего атома | Для автокорреляционной функции номер должен совпадать с номером первого атома | |
| 11 | Номер четвёртого атома | Для автокорреляционной функции номер должен совпадать с номером второго атома |
При задании статистики в текстовом режиме (пример для кросскорреляционной функции):
| Тип статистики | tDistDevCf |
| Номер первого торсионного угла | 1 |
| Номер второго торсионного угла | 2 |
| Номер третьего торсионного угла | 4 |
| Номер четвёртого торсионного угла | 6 |
| Число шагов | 10 |
| Время корреляции, пс | 100 |
| Цвет | 000,000,000 |
| Название графика (обязательно в кавычках) | "DistDevCf" |
| Название файла для данной статистики | DistDevCf.dat |
Таблица 14. Выходной файл для статистики tDistDevCf. Time – время, Corr function – значение корреляционной функции.
Modyp 1.13 build 1a Statistics data file. Data for <DistDevCf> tDistDevCf statistic type Time Corr function +0000.0000 9.4113e-005 +0000.0100 5.4614e-005 ... ... +0049.9900 3.5485e-005 ;Sorry but EOF
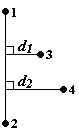
12. tDist2AixCf
Авто- и кросскорреляционная функция отклонения атомов от оси, образованной двумя другими атомами:
| Номер параметра (см. Рис. 16) | Название параметра | Наиболее часто используемое значение | Примечание |
| 3 | Название графика | Любое имя, которое начинается с латинской буквы и имеет длину более двух символов. Имя будет использоваться не только при расчёте, но и при построении графиков с помощью программного пакета Matlab | |
| 4 | Название файла для данной статистики | Задать любое имя файла, которое ранее не было использовано для другой статистики! | |
| 6 | Время корреляции, пс | 100 | Время наблюдения корреляции на протяжении всей траектории |
| 7 | Число шагов | 10 | Число шагов интегрирования, через которое обновляются данные о корреляции |
| 8 | Номер первого атома | Номер угла можно узнать в файле *.str по номеру комментария в строке нужного угла | |
| 9 | Номер второго атома | ||
| 10 | Номер третьего атома | ||
| 11 | Номер четвёртого атома | Для автокорреляционной функции номер должен совпадать с номером третьего атома |
При задании статистики в текстовом режиме (пример для автокорреляционной функции):
| Тип статистики | tDist2AixCf |
| Номер первого торсионного угла | 1 |
| Номер второго торсионного угла | 2 |
| Номер третьего торсионного угла | 4 |
| Номер четвёртого торсионного угла | 4 |
| Число шагов | 10 |
| Время корреляции, пс | 100 |
| Цвет | 000,000,000 |
| Название графика (обязательно в кавычках) | "Dist2AixCf" |
| Название файла для данной статистики | Dist2AixCf.dat |
Таблица 15. Выходной файл для статистики tDist2AixCf. Time – время, Corr function – значение корреляционной функции.
Modyp 1.13 build 1a Statistics data file. Data for <Dist2AixCf> tDist2AixCf statistic type Time Corr function +0000.0000 -5.4397e-002 +0000.0060 -5.6529e-002 ... ... +0049.9980 2.9510e-003 ;Sorry but EOF
Общее количество статистик, которое возможно рассчитывать одновременно, ограничено версией программы и для расширенной версии составляет 30. В окне графического редактора выводится количество оперативной памяти, необходимое для расчёта выбранной статистики (Mem. usage) и всех статистик (Total usage). Если выбрано слишком много статистик, эффективность счёта резко уменьшится. Рекомендуется всегда проверять, сколько памяти нужно для той или иной статистики. Это легко определить, умножив число столбцов (для статистик, где используется эта опция) на 8. Числа записываются в формате double, поэтому на одно число приходится 8 байт памяти.
При расчёте одновременно с файлами статистик (*.dat), создаются файлы контрольных точек для статистик (*.scp), что позволяет продолжить расчёт статистик после остановки счёта.
Запуск Modyp
Программа Modyp написана под Windows. Запуск расчётов осуществляется из окна modyp.
Cначала нужно создать, открыть или отредактировать и сохранить файл с параметрами счёта – prm (вкладка File). Затем создать или отредактировать файл со статистиками tsb (File –> Statistics).
Расчёт запускается с помощью команды Calculations –> Run. Для преждевременной корректной остановки счёта нужно нажать Calculations –> Stop.
Команда Calculatuions –> Freeze во время расчёта траектории на время замораживается счёт и позволяет изменить некоторые параметры и задать новые статистики. При этом запись о них в файле tsb не появляется, то есть после остановки счёта и нового запуска автоматически они считаться не будут. Для того чтобы продолжить считать эти статистики, необходимо повторно внести информацию о них в файл tsb.
Для запуска нескольких файлов в пакетном режиме используется modyp.batch. Его вызов осуществляется командой File –> Batch. Ниже приведён пример файла batch для последовательно запуска расчётов аспарагина, валина и аланина.
;Global presets readprm masn2000.prm var alist create var alist set asn,val,ala for n $alist ifexist $n2000.rlx dontrelax set Calcprm relax 10.00 0.001 500.00 30.00 readstr m$n.str readstat m$n2000.tsb run ;graph_show ;runs calculation label dontrelax next for n $alist set Calcprm resume 10000.00 0.001 500.00 30.00 readstr m$n.str readstat m$n2000.tsb run ;graph_show ;runs calculation next stop ;Stops batch there ;Sorry but EOF
Переменной alist присваиваются значения asn, val и ala. В данном случае параметры счёта для всех остатков совпадают и записаны в файле masn2000.prm.
Сначала проводится релаксация с параметрами, описанными выше для файла prm (set Calcprm relax 10.00 0.001 500.00 30.00). В эту часть modyp.batch можно вносить и другие строки из файла prm. При расчёте они будут использованы вместо тех, что записаны в файле с параметрами. Символы $n заменяются на значения переменной alist. То есть имена файлов должны иметь сходную структуру. Для проверки проведения релаксации вводятся строки ifexist $n2000.rlx dontrelax // shell echo.> $n2000.rlx // label dontrelax. Этими командами осуществляется проверка на наличие файла rlx, который создаётся только в том случае, если релаксация была завершена. Если она была прервана для какого-то расчёта, нужно будет удалить файл trj для этого расчёта и запустить релаксацию заново.
На втором этапе осуществляется расчёт траектории. Его параметры могут быть также заданы в modyp.batch.
До команды stop могут быть заданы и другие циклы.
При запуске необходимо следить, чтобы действительные имена файлов и имена, на которые ссылается modyp.batch совпадали. Если в одном из расчётов имя файла будет отличаться от фактического, данный счёт запущен не будет, а выполнение пакетного файла прекратится.